PID控制器切换到3p-3z控制器的应用与性能分析
摘要
随着电机控制技术的发展,对控制精度和响应速度的要求越来越高。为此,先楫电机控制系统在其硬件电流环中引入了一种新的闭环控制单元(Closed Loop Control, CLC)外设,该外设采用了3p-3z(即三个零点三个极点)类型的控制器。相比传统的PID控制器,3p-3z控制器能够提供更加灵活的频率响应调整能力,适用于更复杂的控制场景。本报告旨在详细介绍先楫电机库新提供的3p-3z控制器特性,包括如何将现有的PID参数转换为3p-3z控制器参数的方法,以及探讨这种转换可能带来的性能变化。
3p-3z控制器概述
3p-3z控制器是一种高级控制算法,它通过设置三个零点和三个极点来实现对系统频率响应的精确调整。与传统的PID控制器相比,3p-3z控制器能够更好地适应非线性系统和具有时变特性的系统,提供更优的动态性能和稳定性。此外,3p-3z控制器还能够在保证系统稳定性的前提下,实现更快的响应速度和更低的稳态误差。
如下图先楫的3p-3z控制器是由一个具有级联的 2P2Z-1P1Z 的控制器构成的
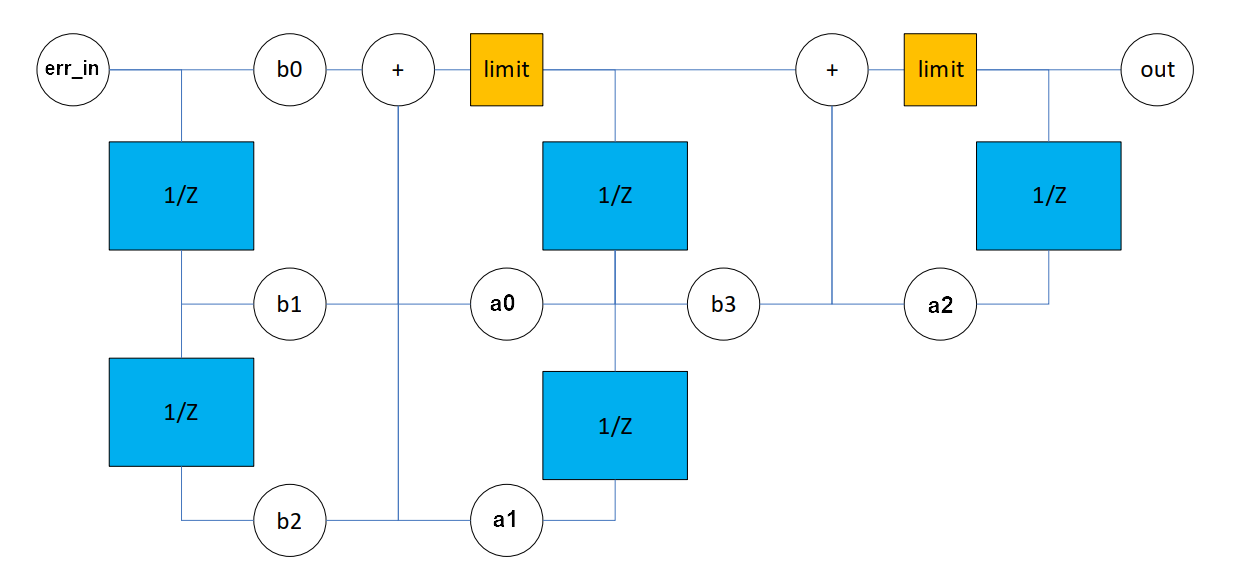
1. 2P2Z 控制器
2P2Z控制器是一种包含两个零点和两个极点的控制算法,主要用于改善系统的频率响应特性。具体来说,2P2Z控制器可以通过调整零点和极点的位置来实现以下功能:
- 提高响应速度:通过合理设置零点位置,可以增强系统的高频响应,使系统能够更快地跟踪目标值。
- 抑制振荡:通过调整极点位置,可以有效抑制系统在高频段的振荡,提高系统的稳定性。
- 补偿相位滞后:2P2Z控制器还可以用于补偿系统中存在的相位滞后问题,特别是在存在大惯性环节的系统中。
2. 1P1Z 控制器
1P1Z控制器则是一个包含一个零点和一个极点的控制算法,主要应用于低频段的控制。它的主要功能包括:
- 低频增益调节:通过调整极点位置,可以改变系统在低频段的增益,从而影响系统的稳态误差。
- 滤波作用:1P1Z控制器可以起到低通滤波的作用,滤除系统中的高频噪声,提高系统的抗干扰能力。
- 相位超前补偿:通过合理设置零点位置,可以在低频段引入相位超前,改善系统的动态响应。
3. 级联 2P2Z-1P1Z 控制器
将2P2Z控制器和1P1Z控制器级联起来,形成一个3p-3z控制器,可以充分利用两者的优点,实现更精细的控制效果。具体来说,这种级联结构的工作原理如下:
- 高频段控制:2P2Z控制器主要负责高频段的控制,通过调整其零点和极点位置,可以显著提高系统的响应速度和稳定性。
- 低频段控制:1P1Z控制器则主要负责低频段的控制,通过调节其极点和零点位置,可以有效改善系统的稳态误差和抗干扰能力。
- 整体协调:两个子控制器之间通过级联的方式协同工作,确保在整个频率范围内都能实现良好的控制性能。
4. 参数设置方法
为了充分发挥3p-3z控制器的性能,合理设置各子控制器的参数至关重要。以下是一些建议的步骤:
- 系统建模:首先对被控对象进行建模,确定系统的传递函数。
- 初步设计:根据系统的需求,初步设定3p3z控制器的零点和极点位置。这一步可以通过经验公式或仿真工具来完成。
- 性能评估:通过仿真或实验,评估控制器的性能,包括响应速度、稳态误差、抗干扰能力等指标。
- 参数优化:根据评估结果,逐步调整各子控制器的参数,直到达到满意的控制效果。
- 稳定性验证:确保最终设计的控制器在所有工作条件下都是稳定的,可以通过根轨迹法或奈奎斯特图等方法进行验证。
离散表达式为
\frac{u(z)}{e(z)} = \left( \frac{b_0 + b_1 z^{-1} + b_2 z^{-2}}{1 - a_0 z^{-1} - a_1 z^{-2}} \right) \cdot \left( \frac{1 + b_3 z^{-1}}{1 - a_2 z^{-1}} \right)PID控制器
离散式PID控制器
离散式PID控制器的输出 u(k) 可以表示为:
u(k) = K_p e(k) + K_i \sum_{i=0}^{k} e(i) T_s + K_d \frac{e(k) - e(k-1)}{T_s}其中:
u(k)是第k个采样时刻的控制输出。e(k)是第k个采样时刻的误差,定义为e(k) = r(k) - y(k),其中r(k)是参考输入,y(k)是系统输出。K_p是比例增益。K_i是积分增益。K_d是微分增益。T_s是采样周期。
增量式PID控制器
增量式PID控制器的输出增量 \Delta u(k) 可以表示为:
\Delta u(k) = K_p [e(k) - e(k-1)] + K_i e(k) T_s + K_d \left( \frac{e(k) - 2e(k-1) + e(k-2)}{T_s} \right)其中:
\Delta u(k)是第k个采样时刻的控制输出增量。e(k)是第k个采样时刻的误差。K_p是比例增益。K_i是积分增益。K_d是微分增益。T_s是采样周期。
对于增量式PID控制器,控制输出 u(k) 通过累加输出增量来更新:
u(k) = u(k-1) + \Delta u(k)PID至3p-3z参数转换方法
为了便于用户从传统PID控制平滑过渡到3p-3z控制,先楫电机库提供了一套的参数转换方法。具体来说,用户只需输入当前使用的PID控制器参数,系统将自动计算出相应的3p-3z参数。注意这种方法只支持增量式PID的转换。所以在参数整定的过程中,建议使用增量式PID。
参数转换使用如下API:
sdk_version: RC1.8
hpm_mcl_stat_t hpm_mcl_pid_to_3p3z(mcl_control_pid_cfg_t *cfg_pid, mcl_clc_coeff_cfg_t *cfg_3p3z)
输入参数为pid的配置信息,由kp,ki,kd组成
输出参数为3p-3z控制器的系数,由b0 b1 b2 b3 a0 a1 a2组成。
同样电机库中给出了增量式pid的软件实现:
hpm_mcl_stat_t hpm_mcl_delta_pid(float setpoint, float feedback, mcl_control_pid_t *pid_x, float *output)
以及位置式pid的实现:
hpm_mcl_stat_t hpm_mcl_position_pid(float setpoint, float feedback, mcl_control_pid_t *pid_x, float *output)
性能评估与分析
为了验证转换后的3p-3z控制器的实际效果,我们进行了仿真,包括但不限于启动时间、稳态误差、抗干扰能力等方面的比较。测试结果显示,在大多数应用场景下,转换后3p-3z控制器均能满足系统的动态响应和稳定性。
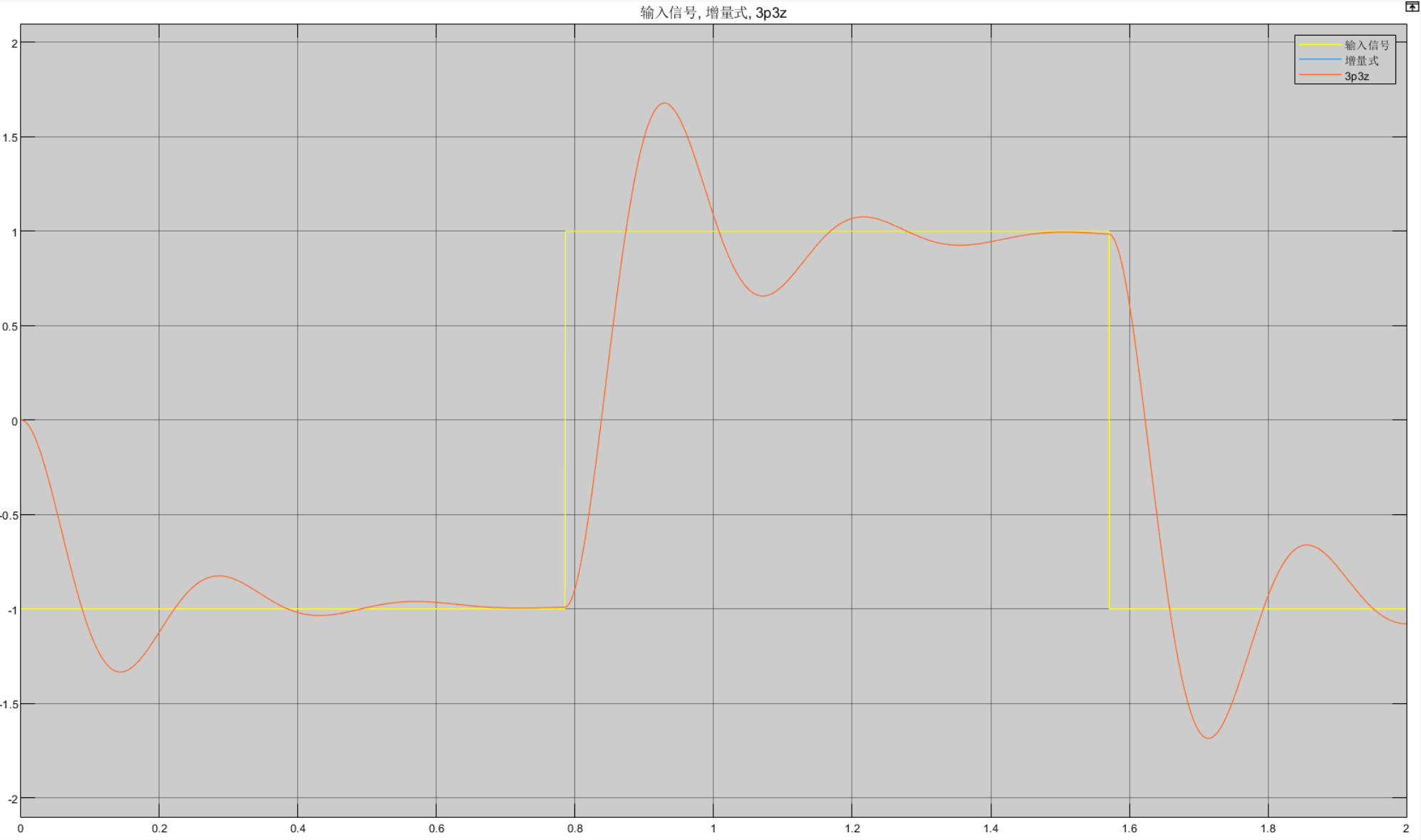
如下为一个简单的Matlab仿真情况:

2个pid控制器使用相同的控制参数,3p-3z控制器的参数使用我们提供的api转换后的参数。控制器的输出给到一个二阶系统的输出作为反馈值给到pid\3p-3z控制器作为输入。
可以看到黄色线为系统的给定,蓝色和红色线分别为增量式PID的系统输出和3p-3z系统的输出,两个曲线完全重合,所以系统的控制器性能一致。
下边再看位置式和增量式的比较:
可以看到在相同的系数下,可以看到系统的瞬态响应基本一致,但是稳态误差会不一致。
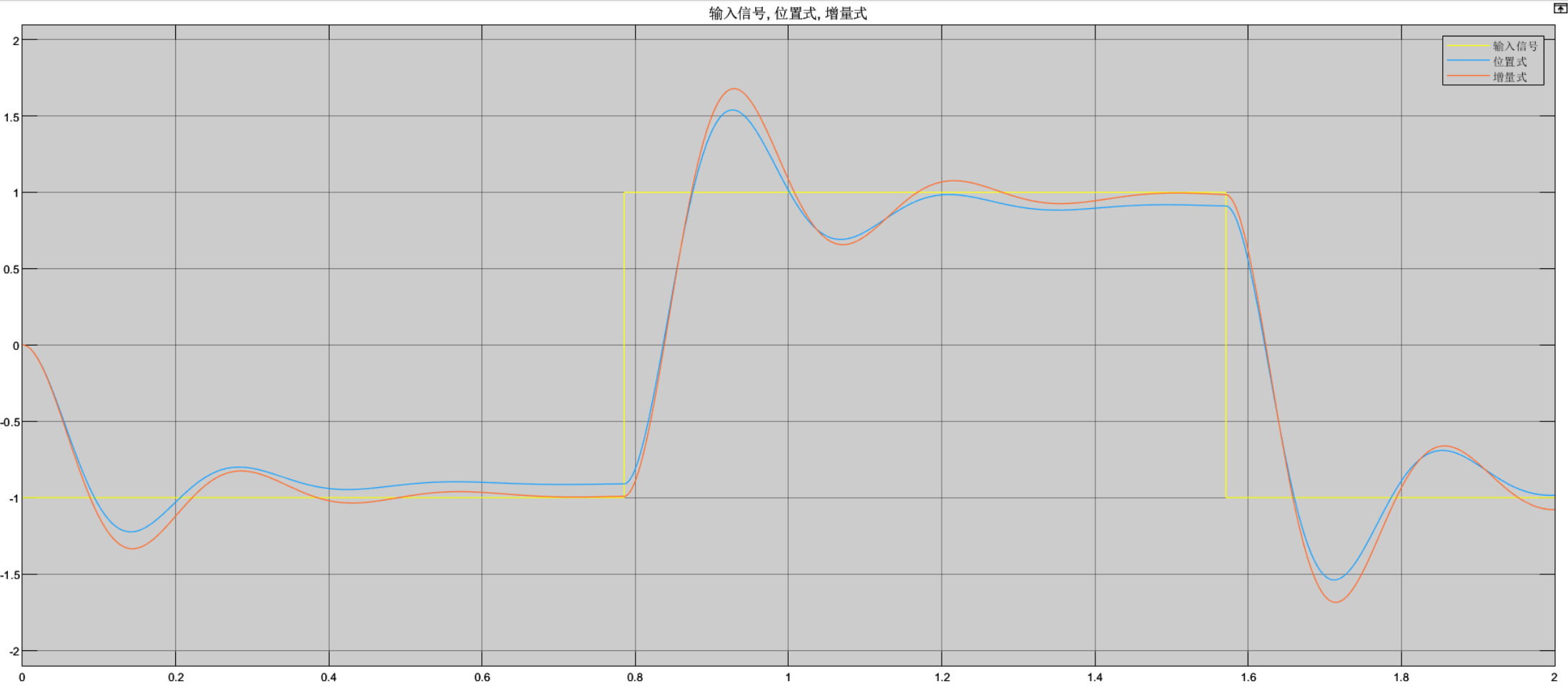
所以位置式pid和3p-3z控制器如果直接转换的化会存在同样的问题,系统的瞬态响应基本一致,但是其他方面会有差异。
结论
先楫电机控制系统通过引入3p-3z控制器,为用户提供了更加高效、灵活的电机控制解决方案。尽管从PID到3p-3z的转换过程中可能存在一定的挑战,但借助于我们提供的参数转换方法,对于增量式PID可以完全替代,对于位置式PID可以部分替代。